・逐次反応
ここでは簡単に三状態の逐次反応を考えましょう
\(\Large \displaystyle \ce{A ->C[k_1] B ->C[k_2] C} \)
その確率密度は,
\(\Large \displaystyle P(x) = \frac{k_1 \cdot k_2}{k_2-k_1} \cdot [exp (-k_1 \ x) - exp (-k_2 \ x)] \)
ここで,係数は規格化(トータル1)のためなので,無視して,間隔dでのヒストグラムでの総和Nは,
\(\Large \displaystyle N = A_0 \sum_{i=0}^ \infty \left[ exp (-k_1 \ d \ i) - exp (-k_2 \ d \ i) \right] \)
と比例係数,A0,を含んだ式となります.
となります.それぞれ独立に積分できるので,
\(\Large \displaystyle y_1 = \sum_{i=0}^\infty \left[ exp (-k_1 \ d \ i) \right] = 1 + exp(-k_1 d) +exp(-2k_1 d) + \cdots \)
\(\Large \displaystyle y_1 \cdot exp (-k_1 \ d )= exp(-k_1 d) +exp(-2k_1 d) + \cdots \)
したがって,
\(\Large \displaystyle y_1 = \frac{1}{1 - exp (-k_1 \ d )} \)
同様に,
\(\Large \displaystyle y_2 = \frac{1}{1 - exp (-k_2 \ d )} \)
となるので,
\(\Large \displaystyle N = A_0 \left\{ \frac{1}{1 - exp (-k_1 \ d )} + \frac{1}{1 - exp (-k_2 \ d )} \right\} \)
\(\Large \displaystyle = A_0 \frac{\{1 - exp (-k_2 \ d )\} - \{1 - exp (-k_1 \ d )\}}{ \{ 1 - exp (-k_1 \ d ) \} \{ 1 - exp (-k_2 \ d ) \} } \)
\(\Large \displaystyle = A_0 \frac{ exp (-k_1 \ d )\} - exp (-k_2 \ d )}{ \{ 1 - exp (-k_1 \ d ) \} \{ 1 - exp (-k_2 \ d ) \} } \)
したがって,
\(\Large \displaystyle A_0 = N \frac{ \{ 1 - exp (-k_1 \ d ) \} \{ 1 - exp (-k_2 \ d ) \} } { exp (-k_1 \ d )\} - exp (-k_2 \ d )}\)
と表すことができます.
・実際の計算
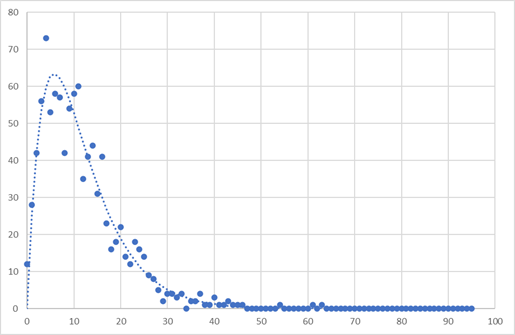
実際に,ランダム関数から指数分布を二つ作成して(詳細はここ),その時間の和’をとりました.,k,dを色々変えて計算させると,
k1=0.15, k2=0.2, d=1, N=1000, -> A0=0.602, Peak=63.44

k1=0.15, k2=0.2, d=1.5, N=1000, -> A0=0.905, Peak=95.457
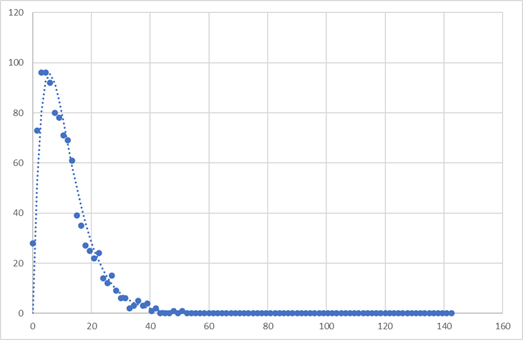
k1=0.1, k2=0.2, d=1.5, N=1000, -> A0=0.301, Peak=75.282
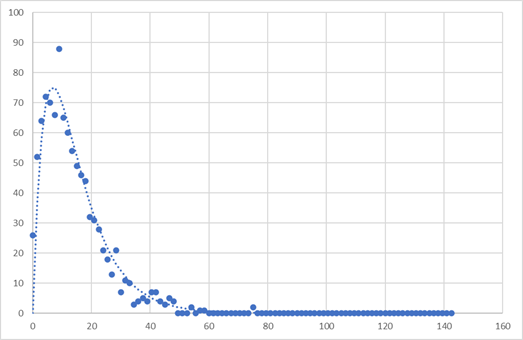
ときれいにフィットできました.
次は,正規分布,の場合です.